Recursion and Machine Language

Hanoi Towers

Recursive Algorithm in 8088 DEBUG

The first time I implemented the algorithm to solve the Hanoi Towers puzzle I was learning Pascal, and it was obviously the language I chose to do it. Some time later, I came across an old Motorola 6800 microprosessor development kit and went on and implemented the algorithm by assembling it on paper and punching in the machine codes with an hexadecimal keypad. The output was a 7 segment display!

There is nothing extraordinary about this, except for the fact that I applied a recursive algorithm directly in 6800uP machine language. I had two motivations for doing this: first, the recursive solution is very simple and required less coding and second, I was sick of all the buzz about "recursive languages" and how "magic" they were, and how dumb those "other", "non-recursive" languges were.

So, let's kick some computer nazis's but!

Fig. 1 Recursive Hanoi Algorithm in 8088 Assembly

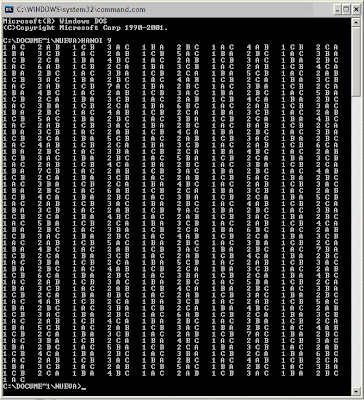
Recently, I was teaching Excel VBA to a group of students and thought it would be fun to implement the Hanoi algorithm and use Excel graphics to show the "disks". I actualy did it and was really fun and exiting for the students who had never used Excel like that. I went on and thought why not relive the experience, but this time, with a modern PC type computer with display, keyboard and "debug.com" as the "assembler". Fig. 1 shows a "deluxe" version of the program which takes line parameters (N=3 to 9, otherwise assumes the default 3 disks) and prints new line characters.

Much Easier!

The following C++ code shows an implementation of the classical recursive solution. I intentionally defined the variables AX, DX and CX since those registers would be used in my assembly code.

The Algorithm in C

#include <stdio.h> void h(int N, char AX, char DX, char CX) { if (N>0) { h(N-1, AX, CX, DX); printf("%d %c %c\n", N, AX, DX); h(N -1,CX, DX, AX); } } void main() { h(3, 'A','C', 'B'); }

• The poles A (source), B (intermediate) and C (destination) would go respectively to AX, CX and DX. Shame: such a waste!.
• C++ parameters are: N (number of disks), AX (source), DX (destination) and CX (intermediate).
• Notice that the first call to de procedure from the main program assigns each variable its "correct" pole. However, inside the procedure, there are two recursive calls with two parameters swapped in each respective call: The first call decrements N and swaps CX and DX (exchanges destination and intermediate). The second call decrements N and swaps AX and CX (exchanges source an intermediate). Between these two procedure calls, it prints N, AX (source) and DX (destination).
• The fact that the procedure calls itself may seem a little awkward to follow at firs glance, but it actually is very straight forward.

Lets follow the example shown in the above C++ code: N=3, AX='A', DX='C' and CX='B'

Table I The state of "variables" on the run

The Assembly Code

This is the actual assembly code that fully implements the algorithm (see Fig. 2). Afterwards I created a "deluxe" version wich is shown in Fig. 1; is the same basic code with the addition of initialization code to accept N as a line parameter and an a little procedure to print new lines.

Fig. 2 DEBUG'S Recursive Hanoi First Run

Complete Listing in "Debugese"

NHANOI.COM A DW 0 DW 0 DW 0 DW 0 MOV AX,11 MOV CX,12 MOV DX,13 MOV BX,4 CALL 11C MOV AX,4C INT 21 CMP BX,0 JE 173 PUSH DX PUSH CX PUSH AX PUSH BX DEC BX MOV [106],DX MOV DX,CX MOV CX,[106] CALL 11C POP BX POP AX POP CX POP DX MOV [102],AX MOV [104],CX MOV [106],DX CALL 174 DEC BX MOV [100],BX MOV BX,[102] CALL 174 MOV BX,[106] CALL 174 MOV BX,[100] MOV AX,[102] MOV CX,[104] MOV DX,[106] MOV [102],AX MOV AX,CX MOV CX,[102] CALL 11C RET MOV AH,2 MOV DX,BX ADD DX,30 INT 21 MOV DX,20 INT 21 RET RCX 95 W Q

The Saga Continues...

Don't Miss It:

SEE HERE: HANOI GOES BABYLON!

Sergio Otaño